Informatyka

Temat: Badanie własności liczb całkowitych. Sortowanie bąbelkowe.

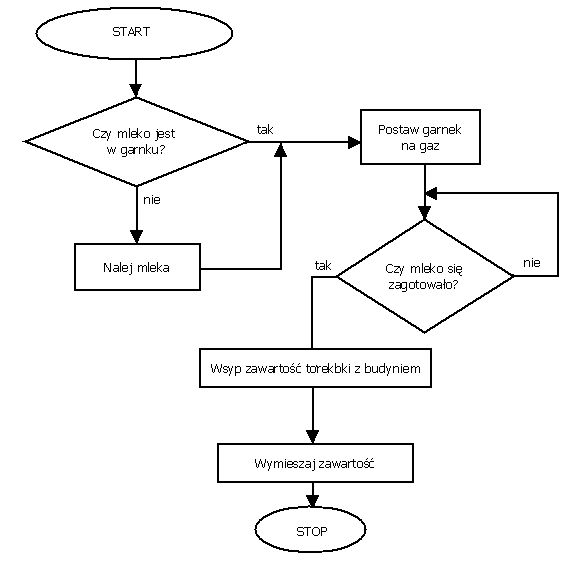
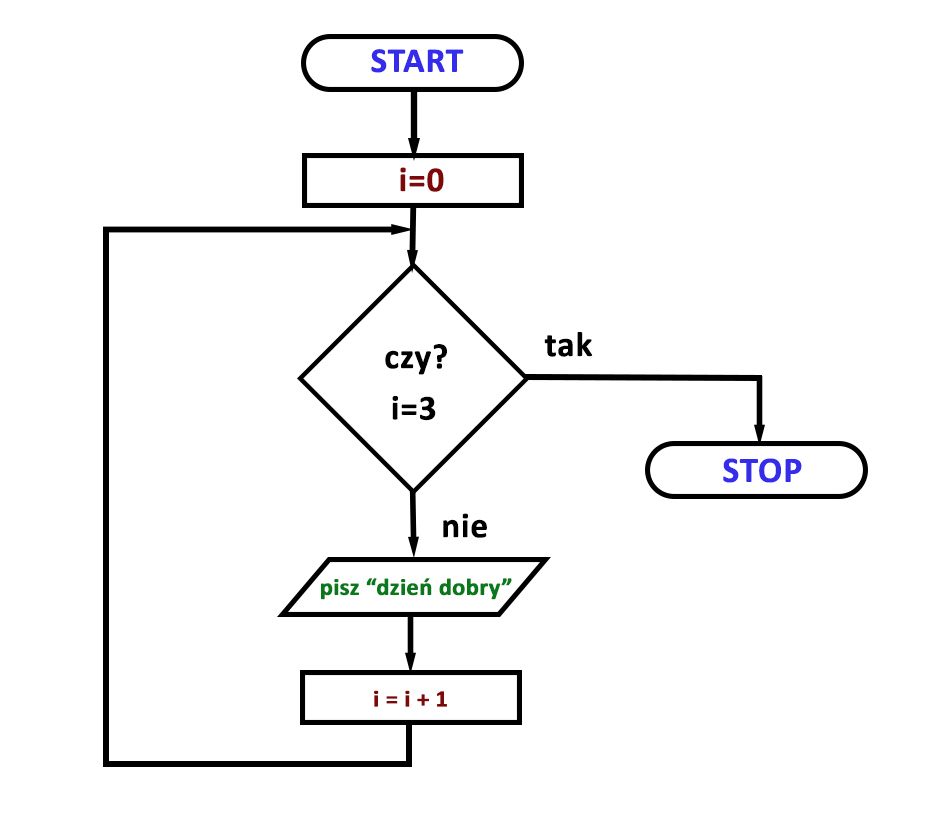
Czym jest programowanie?

Programowanie to umiejętność rozmowy z komputerem. Rozmawiamy z komputerem w zrozumiałych dla niego językach, czyli językach programowania. Dajemy komputerowi polecenia, co ma zrobić, a on w odpowiedzi pokazuje nam wyniki swojej pracy. Osobę, która programuje, nazywamy programistą lub developerem.

Algorytmy – skończony ciąg jasno zdefiniowanych czynności koniecznych do wykonania pewnego rodzaju zadań, sposób postępowania prowadzący do rozwiązania problemu. Można go przedstawić na schemacie blokowym.

Zadaniem algorytmu jest przeprowadzenie systemu z pewnego stanu początkowego do pożądanego stanu końcowego. Badaniem algorytmów zajmuje się algorytmika. Algorytm może zostać zaimplementowany w postaci programu komputerowego.
Jako przykład stosowanego w życiu codziennym algorytmu podaje się często przepis kulinarny. Dla przykładu, aby ugotować bigos, należy w określonej kolejności oraz odstępach czasowych (imperatyw czasowy) dodawać właściwe rodzaje kapusty i innych składników. Może istnieć kilka różnych przepisów dających na końcu bardzo podobną potrawę. Algorytmy zwykle formułowane są w sposób ścisły w oparciu o język matematyki.
                    
Znajdowanie liczb pierwszych metodą sita Eratostenesa - liczby pierwsze można wyszukiwać poprzez eliminację ze zbioru liczbowego wszystkich wielokrotności wcześniejszych liczb.

Mamy następujący zbiór liczb naturalnych:

{2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50}

Ze zbioru wyrzucamy wszystkie wielokrotności pierwszej liczby 2. Otrzymujemy następujący zbiór:

{2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50}

W zbiorze pozostały liczby nieparzyste – z wyjątkiem pierwszej liczby 2. Liczby podzielne przez dwa zostały wyeliminowane. Teraz eliminujemy wielokrotności kolejnej liczby 3. Otrzymamy następujący zbiór:

{2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 }

Teraz w zbiorze pozostały liczby niepodzielne przez 2 i 3 – z wyjątkiem pierwszych 2 i 3. Zwróć uwagę, iż kolejna liczba 4 została już ze zbioru wyeliminowana. Skoro tak, to ze zbioru zniknęły również wszystkie wielokrotności liczby 4, ponieważ są one również wielokrotnościami liczby 2, a te wyeliminowaliśmy przecież na samym początku. Przechodzimy zatem do liczby 5 i eliminujemy jej wielokrotności otrzymując zbiór wynikowy:

{2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 }

Oprócz 2, 3 i 5 pozostałe w zbiorze liczby nie dzielą się już przez 2, 3 i 5. Liczba 6 jest wyeliminowana (wielokrotność 2 ), zatem przechodzimy do 7. Po wyeliminowaniu wielokrotności liczby 7 zbiór przyjmuje postać:

{2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 }

W zbiorze pozostały same liczby pierwsze.

{2 3 4 5 6 7 89 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 }

Powyższe operacje wyrzucania wielokrotności prowadzą do przesiania zbioru wejściowego. W zbiorze pozostają tylko liczby pierwsze, liczby będące wielokrotnościami poprzedzających je liczb zostają ze zbioru odsiane. Algorytm dokonujący tej eliminacji nosi nazwę sita Eratostenesa (ang. Eratosthenes' sieve ) i jest jednym z najszybszych sposobów generowania liczb pierwszych.



Przykład - Sito Eratostenesa w Pythonie 
n = int(input('n = '))
if n < 2:
    print("Brak liczb pierwszych w podanym zakresie")
else:
    skr = [False] * (n + 1)
    i = 2
    while i * i <= n:
        if  not skr[i]:
            j = i * i
            while j <= n:
                skr[j] = True
                j += i
        i += 1
    for i in range(2, n+1):
        if not skr[i]:
            print(i, end = " ")
Sortowanie danych. Sortowanie metodą bąbelkową

Algorytm sortowania bąbelkowego jest jednym z najstarszych algorytmów sortujących. Można go potraktować jako ulepszenie opisanego w poprzednim rozdziale algorytmu sortowania głupiego. Zasada działania opiera się na cyklicznym porównywaniu par sąsiadujących elementów i zamianie ich kolejności w przypadku niespełnienia kryterium porządkowego zbioru. Operację tę wykonujemy dotąd, aż cały zbiór zostanie posortowany.

ObiegZbiórOpis operacji
1
 5 4 3 2 1
Rozpoczynamy od pierwszej pary, która wymaga wymiany elementów 
 4 5 3 2 1
Druga para też wymaga zamiany elementów
 4 3 5 2 1
Wymagana wymiana elementów
 4 3 2 5 1
Ostatnia para również wymaga wymiany elementów
 4 3 2 1 5
Stan po pierwszym obiegu. Zwróć uwagę, iż najstarszy element (5) znalazł się na końcu zbioru, a najmłodszy (1) przesunął się o jedną pozycję w lewo.
2
 4 3 2 1 5
Para wymaga wymiany
 3 4 2 1 5
Para wymaga wymiany
 3 2 4 1 5
Para wymaga wymiany
 3 2 1 4 5
Elementy są w dobrej kolejności, zamiana nie jest konieczna.
 3 2 1 4 5
Stan po drugim obiegu. Zwróć uwagę, iż najmniejszy element (1) znów przesunął się ojedną pozycję w lewo. Z obserwacji tych można wywnioskować, iż po każdym obiegu najmniejszy element wędruje ojedną pozycję ku początkowi zbioru. Najstarszy element zajmuje natomiast swe miejsce końcowe.
3
 3 2 1 4 5
Para wymaga wymiany
 2 3 1 4 5
Para wymaga wymiany
 2 1 3 4 5
Dobra kolejność
 2 1 3 4 5
Dobra kolejność
 2 1 3 4 5
Stan po trzecim obiegu. Wnioski te same.
4
 2 1 3 4 5
Para wymaga wymiany
 1 2 3 4 5
Dobra kolejność
 1 2 3 4 5
Dobra kolejność
 1 2 3 4 5
Dobra kolejność
 1 2 3 4 5
Zbiór jest posortowany. Koniec

Posortowanie naszego zbioru wymaga 4 obiegów. Jest to oczywiste: w przypadku najbardziej niekorzystnym najmniejszy element znajduje się na samym końcu zbioru wejściowego. Każdy obieg przesuwa go o jedną pozycję w kierunku początku zbioru. Takich przesunięć należy wykonać n - 1 (n - ilość elementów w zbiorze).

Uwaga:

Algorytm sortowania bąbelkowego jest uważany za bardzo zły algorytm sortujący. Można go stosować tylko dla niewielkiej liczby elementów w sortowanym zbiorze (do około 5000). Przy większych zbiorach czas sortowania może być zbyt długi.



Przykład - Sortowanie metodą bąbelkową w Pythonie 

def wypiszTablice(t):  # pomocnicza funkcja do szybkiego wypisania zawartosci tablicy
    for el in t:
        print(el, end=" | ")


print("Program sortujacy tablice metoda babelkowa")
print("Podaj ilosc elementow tablicy: ")
n = int(input())  # pobieramy ilosc elementow od uzytkownika
tab = []  # tworzymy pusta tablice, do ktorej bedziemy dodawac kolejne elementy
for i in range(n):
    print("Podaj element nr. " + str(i))  # pobieramy kolejne elementy od uzytkownika
    tab.append(float(input()))  # zwroc uwage, ze pobieramy elementy typu rzeczywistego
print("Wprowadzona tablica:")
wypiszTablice(tab)
zmian = 1  # zmienna pomocnicza
for i in range(n - 1):  # iterujemy przez tablice
    if zmian == 0:  # jezeli w poprzednim kroku nie dokonano zadnych zmian w tablicy(co oznacza ze jest juz posortowana)
        break  # przerywamy jej dzialanie
    zmian = 0  # w przeciwnym razie resetujemy licznik zmian
    for j in range(n - 1):  # iterujemy poprzez pozostale elementy tablicy
        if tab[j] > tab[j + 1]:  # jezeli element jest j jest wiekszy od elementu j+1
            tab[j], tab[j + 1] = tab[j + 1], tab[j]  # zamieniamy je miejscami
            zmian += 1  # i zwiekszamy ilosc zmian o 1
print("Posortowana tablica:")
wypiszTablice(tab)


Powinieneś umieć: